-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX2 Marathon (archive) (3 Viewers)
- Thread starter nightweaver066
- Start date
Re: 2012 HSC MX2 Marathon
The equation of the ellipse is the top semi-ellipse
Covering the first two quadrants. Now when you sub
Y=mx+c into semi ellipse and form a quadratic in x
The y int of the tangent must be positive otherwise
It can't be a tangent to the top semi ellipse so c>0, now
As for m<0 there is only one possible way this can
Occur and that is if the x coordinate of the point of
Contact of the tangent is positive. This is deduced if
You find the x value of the point of contact using
The double root method, and this shows the x value of the
Poiny of contact is positive if m<0 otherwise the x value
Will be negative, so this condition for m can't occur unless
The tangent interests in the first quadrant
The equation of the ellipse is the top semi-ellipse
Covering the first two quadrants. Now when you sub
Y=mx+c into semi ellipse and form a quadratic in x
The y int of the tangent must be positive otherwise
It can't be a tangent to the top semi ellipse so c>0, now
As for m<0 there is only one possible way this can
Occur and that is if the x coordinate of the point of
Contact of the tangent is positive. This is deduced if
You find the x value of the point of contact using
The double root method, and this shows the x value of the
Poiny of contact is positive if m<0 otherwise the x value
Will be negative, so this condition for m can't occur unless
The tangent interests in the first quadrant
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
MOAR CONICS!!
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}@plus;\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx@plus;c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}@plus;\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" title="\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" /></a>
MOAR CONICS!!
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}@plus;\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx@plus;c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}@plus;\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" title="\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" /></a>
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Last edited:
OMGITzJustin
Well-Known Member
- Joined
- Jun 28, 2010
- Messages
- 1,002
- Gender
- Male
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
what is the best method of graphing 1/f(x) graphs? for example 1/sinx?
what is the best method of graphing 1/f(x) graphs? for example 1/sinx?
Re: 2012 HSC MX2 Marathon
note when f(x) equals 0 there becomes vertical asymptotes. Also the turning points on f(x) stay the same, only the y value changes
and the type of turning point reverses
f(x) represents the y values and 1/f(x) means 1 over every y value. So you use limits as f(x) appraoches 0 and infinity andwhat is the best method of graphing 1/f(x) graphs? for example 1/sinx?
note when f(x) equals 0 there becomes vertical asymptotes. Also the turning points on f(x) stay the same, only the y value changes
and the type of turning point reverses
- Joined
- Feb 16, 2005
- Messages
- 8,518
- Gender
- Male
- HSC
- 2006
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Re: 2012 HSC MX2 Marathon
question kinda hints to use GP
Noting that for
for 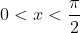 , see that:
, see that:
} dx = \int \frac{\cos x}{1-\sin x} dx=\int \cos x \sum_{n=0}^\infty \sin^n x dx )
Assuming interchangeability between integral and summation, the result follows easily.
question kinda hints to use GP
Noting that
Assuming interchangeability between integral and summation, the result follows easily.
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
Re: 2012 HSC MX2 Marathon
 dx)
\right]_0^d)

Then as d approaches pi/2, cosd -> 0, and tand + secd -> positive infinity. So its pretty clear that the integral has to diverge
No its not...Trebla's original question with limits 0 --> pi/2 was actually convergent. Just because a point is undefined, does not necessarily mean that the area is automatically infinite.
Then as d approaches pi/2, cosd -> 0, and tand + secd -> positive infinity. So its pretty clear that the integral has to diverge
Last edited:
Re: 2012 HSC MX2 Marathon
Sides then applying l hopitals rule
Will show this is actually convergent
As carrot said
This does seem true, but e ing bothNo its not...
Then as d approaches pi/2, cosd -> 0, and tand + secd -> positive infinity. So its pretty clear that the integral has to diverge
Sides then applying l hopitals rule
Will show this is actually convergent
As carrot said
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Beforehand I was being lazy and checked the convergence using Wolfram (which claimed it converges and actually gave a value) instead of actually verifying it by hand.
Never again will I trust it for anything more than simple calculations ^^
Beforehand I was being lazy and checked the convergence using Wolfram (which claimed it converges and actually gave a value) instead of actually verifying it by hand.
Never again will I trust it for anything more than simple calculations ^^
Re: 2012 HSC MX2 Marathon
I don't want to spoil the party but...
Any chance we could have questions more orientated towards a regular MX2 student, or a little harder, but something that most should at least be able to attempt. A lot of people would probably be scared off, especially since you guys are into or out of uni maths already!
I don't want to spoil the party but...
Any chance we could have questions more orientated towards a regular MX2 student, or a little harder, but something that most should at least be able to attempt. A lot of people would probably be scared off, especially since you guys are into or out of uni maths already!
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Find the value of:
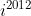
OR
Find the value of:
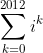
Even better:
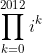
Something I predict will appear in either the school Trials or the Complex Number exam term test (verified appeared in already 3 schools as per my prediction last year haha):I don't want to spoil the party but...
Any chance we could have questions more orientated towards a regular MX2 student, or a little harder, but something that most should at least be able to attempt. A lot of people would probably be scared off, especially since you guys are into or out of uni maths already!
Find the value of:
OR
Find the value of:
Even better:
Last edited:

