Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 2U Marathon
x^{n+1} ) converges to zero
converges to zero
One way is that:
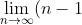x^{n+1} = \lim_{n \to \infty} nx^{n+1} - \lim_{n \to \infty} x^{n+1} )
We know the second limit converges to zero, because^n = 0 ) (sketch the graph of 2^(-n))
(sketch the graph of 2^(-n))
Yep well done, however for the last part I would have liked some better justification of how the term,View attachment 28510 I hope it's correct... may not be thoughlol
One way is that:
We know the second limit converges to zero, because

