-
Looking for HSC notes and resources? Check out our Notes & Resources page
How do you derive this? (1 Viewer)
- Thread starter enigma_1
- Start date
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Do you mean differentiate? If so, did you mean:
 ?
?
You need to differentiate both sides with respect to x, remembering that y is a function of x - i.e.) so then apply this knowledge when you do:
so then apply this knowledge when you do:
) = \dfrac{d}{dx}(7)) - remembering to use chain rule/product rule where needed
- remembering to use chain rule/product rule where needed
You need to differentiate both sides with respect to x, remembering that y is a function of x - i.e.
panda15
Alligator Navigator
- Joined
- Feb 22, 2012
- Messages
- 673
- Gender
- Male
- HSC
- 2013
Yeah the method that asianese showed is implicit differentiation, which only comes up in Extension 2.WHOa ok I've never done this before, can you please show me the method?sorry
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
I'll show you the method anyway - the process is called 'implicit differentiation' because y is 'implicitly' - (NOT explicitly - y is not the subject here!) defined as a function of x. (We usually assume y is a function of x anyway)
So in the normal way, we can apply the 'differentiation operator',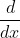 to both sides of the function. Our goal is to find
to both sides of the function. Our goal is to find 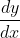 .
.
Now we have
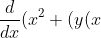)^2-x^2y(x) = \dfrac{d}{dx}(7)) and differentiating term by term, we get that
and differentiating term by term, we get that
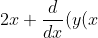)^2) - \dfrac{d}{dx}(x^2(y(x))) = 0) . Now, we consider the first term in y^2 - use the chain rule. Remember if we had something like
. Now, we consider the first term in y^2 - use the chain rule. Remember if we had something like 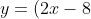^4) , to differentiate, bring down the power, then multiply by the derivative of the inside function. Do the same with y^2, except the 'inside function' is actually y itself, so its derivative is indeed
, to differentiate, bring down the power, then multiply by the derivative of the inside function. Do the same with y^2, except the 'inside function' is actually y itself, so its derivative is indeed 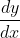 . Repeat this process with the second term in x^2y, but remember this will have to ulilise the product rule - x^2 is multiplied by y, as well as a chain rule, since y is a function of x.
. Repeat this process with the second term in x^2y, but remember this will have to ulilise the product rule - x^2 is multiplied by y, as well as a chain rule, since y is a function of x.
Once we have all our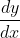 s appearing, collect all these on one side and rearrange to produce the result.
s appearing, collect all these on one side and rearrange to produce the result.
The final answer should be}{2y-x^2})
So in the normal way, we can apply the 'differentiation operator',
Now we have
Once we have all our
The final answer should be
Last edited:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
What textbook?Wow thanks man!! So you're certaini that this wont be tested in MX1 exams yeah? It was in a MX1 textbook - odd..
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
It is a MX2 technique - not in the 2/3U syllabi.What? I learnt implicit differentiation in year 11 MX1. It's not a MX2 technique :S
enigma_1
~~~~ Miss Cricket ~~~~
Whaaaat now I'm really confused?! This thing was from Terry Lee.
There is actually a chapter on implicit diff in Cambridge but it says Extension or something.
@QZP, were you ever tested in an exam on it?
There is actually a chapter on implicit diff in Cambridge but it says Extension or something.
@QZP, were you ever tested in an exam on it?
panda15
Alligator Navigator
- Joined
- Feb 22, 2012
- Messages
- 673
- Gender
- Male
- HSC
- 2013
Your teacher probably taught it to you because it isn't a difficult concept, and it can help with some of the nastier 3U differentials, but it is a 4U technique. 3U will never get a question that involves implicit differentiation.What? I learnt implicit differentiation in year 11 MX1. It's not a MX2 technique :S
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Whaaaat now I'm really confused?! This thing was from Terry Lee.
There is actually a chapter on implicit diff in Cambridge but it says Extension or something.
@QZP, were you ever tested in an exam on it?
Terry Lee has a habit of not reading syllabi when he writes textbooks. Ignore it.
Oh okay, I didn't know it was part of MX2. Thanks 
@Hyper_bole
I wasn't tested on it, but honestly it's not all that hard to learn. And it makes the whole process of differentiation a lot cleaner (viewing d/dx as an operator vs. as a limiting process by first principles). I'd recommend knowing it whether or not it's in your test
@Hyper_bole
I wasn't tested on it, but honestly it's not all that hard to learn. And it makes the whole process of differentiation a lot cleaner (viewing d/dx as an operator vs. as a limiting process by first principles). I'd recommend knowing it whether or not it's in your test
Kiraken
RISK EVERYTHING
- Joined
- Jun 8, 2012
- Messages
- 1,905
- Gender
- Undisclosed
- HSC
- N/A
some people learn it in Extension 1 because as pointed out elsewhere in this thread it is in a chapter as an "extension" topic in the cambridge prelim 3u book. It is technically within mx2 but by that stage you should have the mathematical knowledge to understand it so you can learn it now but it is unlikely to be examinable in a 3u exam (although if your school makes it's own exams and you went through this topic at school it is best to confirm with the teacher if it will be examined)What? I learnt implicit differentiation in year 11 MX1. It's not a MX2 technique :S
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,757
- Gender
- Male
- HSC
- 2013
Don't worry about it.
You will NEVER get this in a MX1 HSC paper.
It is too unfair.
You will NEVER get this in a MX1 HSC paper.
It is too unfair.
