-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX2 Marathon (archive) (5 Viewers)
- Thread starter nightweaver066
- Start date
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
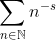
ONLY for s with real part larger than one. It turns out there is only one "nice" function that is defined on the whole complex plane (excluding s=1) that agrees with this infinite series wherever the latter converges. THIS is the function that is conjectured to have all nontrivial zeros on the line Re(s)=1/2.
Okay, I see what you are asking. This is a common misconception. The Riemann Zeta function is defined by the series:I don't want to make a thread about this as i could just ask it here. How can a complex function that converges for Re(z)>s where s is a real number have a zero for Re(z)<s. I don't understand the logic and was wondering if the initial statement of convergence must be wrong as a imaginary part of high enough value might change the nature of the limit to infinity. I basically stumbled across this while reading about Reimanns zeta function which converges for Re(S)>1 but has zeroes at Re(s)=1/2 which seems like a contradiction.
ONLY for s with real part larger than one. It turns out there is only one "nice" function that is defined on the whole complex plane (excluding s=1) that agrees with this infinite series wherever the latter converges. THIS is the function that is conjectured to have all nontrivial zeros on the line Re(s)=1/2.
lolcakes52
Member
- Joined
- Oct 31, 2011
- Messages
- 283
- Gender
- Undisclosed
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
So what your saying is that it only definitely converges for Re(s)>1 but can converge for values less than or equal to one depending on the imaginary part? In this case it can converge but only for specific values of Im(s)<1 ?
So what your saying is that it only definitely converges for Re(s)>1 but can converge for values less than or equal to one depending on the imaginary part? In this case it can converge but only for specific values of Im(s)<1 ?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
No, the series I wrote down converges if and ONLY if Re(s)>1. It diverges everywhere else. However, this fragment of a function can be extended to the whole complex plane in a very natural way. (Excluding the point s=1). This process is called analytic continuation and is a recurring theme in complex analysis.
No, the series I wrote down converges if and ONLY if Re(s)>1. It diverges everywhere else. However, this fragment of a function can be extended to the whole complex plane in a very natural way. (Excluding the point s=1). This process is called analytic continuation and is a recurring theme in complex analysis.
Re: 2012 HSC MX2 Marathon
It actually is a VERY difficult theorem to prove.
Prove analytic continuation.This process is called analytic continuation and is a recurring theme in complex analysis.
It actually is a VERY difficult theorem to prove.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Given that:
^n )
Show that:
^n )
Given that:
Show that:
Re: 2012 HSC MX2 Marathon
damn you carrotGiven that:
Show that:
^n )
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
Which theorem are you referring to? The Monodromy theorem? It isn't too difficult to find the analytic continuation of the zeta function in particular...Prove analytic continuation.
It actually is a VERY difficult theorem to prove.
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Going off Carrot's question, this is to prove the first result (from Cambridge):
<img src="http://latex.codecogs.com/gif.latex?\textup{Consider the area under }y=\frac{1}{x}\textup{ between x=n and x=n+1}\\ a) \textup{ Show that }\frac{1}{n+1}< \int_{n}^{n+1}\frac{1}{x}dx< \frac{1}{n}\\ b)\textup{ Hence show that }\frac{n}{n+1}< ln(1+\frac{1}{n})^n< 1\\ c)\textup{ Take the limit of this last result as n tends to infinity to}\\ \textup{show that }\lim_{n \to \infty }(1+\frac{1}{n})^n=e" title="\textup{Consider the area under }y=\frac{1}{x}\textup{ between x=n and x=n+1}\\ a) \textup{ Show that }\frac{1}{n+1}< \int_{n}^{n+1}\frac{1}{x}dx< \frac{1}{n}\\ b)\textup{ Hence show that }\frac{n}{n+1}< ln(1+\frac{1}{n})^n< 1\\ c)\textup{ Take the limit of this last result as n tends to infinity to}\\ \textup{show that }\lim_{n \to \infty }(1+\frac{1}{n})^n=e" />
Going off Carrot's question, this is to prove the first result (from Cambridge):
<img src="http://latex.codecogs.com/gif.latex?\textup{Consider the area under }y=\frac{1}{x}\textup{ between x=n and x=n+1}\\ a) \textup{ Show that }\frac{1}{n+1}< \int_{n}^{n+1}\frac{1}{x}dx< \frac{1}{n}\\ b)\textup{ Hence show that }\frac{n}{n+1}< ln(1+\frac{1}{n})^n< 1\\ c)\textup{ Take the limit of this last result as n tends to infinity to}\\ \textup{show that }\lim_{n \to \infty }(1+\frac{1}{n})^n=e" title="\textup{Consider the area under }y=\frac{1}{x}\textup{ between x=n and x=n+1}\\ a) \textup{ Show that }\frac{1}{n+1}< \int_{n}^{n+1}\frac{1}{x}dx< \frac{1}{n}\\ b)\textup{ Hence show that }\frac{n}{n+1}< ln(1+\frac{1}{n})^n< 1\\ c)\textup{ Take the limit of this last result as n tends to infinity to}\\ \textup{show that }\lim_{n \to \infty }(1+\frac{1}{n})^n=e" />
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
^n$. \\ \\We shall show $\log(x_n)\rightarrow x$ as $n\rightarrow\infty$.\\ \\ $\log(x_n)=x\cdot\frac{\log(1+x/n)}{x/n}$\\by rearrangement. \\ \\So as $n\rightarrow\infty$ we get:\\ \lim_{n\rightarrow\infty}\log(x_n)=x\cdot\lim_{y\rightarrow0}\frac{\log(1+y)-\log(1)}{y}=x\cdot\frac{d}{dt}(\log(t))|_{t=1}=x.$)
Don't know what you are expecting us to assume, as arbitrary real powers are not defined in the HSC. But we can make sense of the question using the integral definition of the logarithm, and the log laws/differentiation laws that follow.Given that:
Show that:
^n )
Last edited:
Cyberbully
Where do you live?
- Joined
- Oct 29, 2011
- Messages
- 122
- Gender
- Undisclosed
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
How would you approach this algebraically (or any general explanation for that matter):
<img src="http://latex.codecogs.com/gif.latex?\textup{find the locus of } arg(z(z-(\sqrt{3} + i))) = \frac{\pi}{6}" title="\textup{find the locus of } arg(z(z-(\sqrt{3} + i))) = \frac{\pi}{6}" />
How would you approach this algebraically (or any general explanation for that matter):
<img src="http://latex.codecogs.com/gif.latex?\textup{find the locus of } arg(z(z-(\sqrt{3} + i))) = \frac{\pi}{6}" title="\textup{find the locus of } arg(z(z-(\sqrt{3} + i))) = \frac{\pi}{6}" />
Last edited:
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Do it geometrically:
<img src="http://latex.codecogs.com/gif.latex?arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" title="arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" />
Try going from here. Tell us how you go (I haven't tried the question yet so I don't know the answer.
Do it geometrically:
<img src="http://latex.codecogs.com/gif.latex?arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" title="arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" />
Try going from here. Tell us how you go (I haven't tried the question yet so I don't know the answer.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
)) = \arg(z) + \arg(z-(\sqrt{3}+i)) \qquad $using a property of the argument.$)
Try it from here.
And beaten to it.
How would you approach this algebraically (or any general explanation for that matter):
find the locus of arg(z(z-(sqrt(3)+i))) = pi/6
Try it from here.
And beaten to it.
Cyberbully
Where do you live?
- Joined
- Oct 29, 2011
- Messages
- 122
- Gender
- Undisclosed
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
didn't get very far.
the "answer" is a straight line through origin and (sqrt(3) + i), excluding the point (sqrt(3) + i) on an argand diagram if it helps...
tried that.Do it geometrically:
<img src="http://latex.codecogs.com/gif.latex?arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" title="arg(z(z-(\sqrt{3}+i))=\frac{\pi}{6}\\ argz+arg(z-(\sqrt{3}+i))=\frac{\pi}{6}" />
Try going from here. Tell us how you go (I haven't tried the question yet so I don't know the answer.
didn't get very far.
the "answer" is a straight line through origin and (sqrt(3) + i), excluding the point (sqrt(3) + i) on an argand diagram if it helps...
Re: 2012 HSC MX2 Marathon
Assume a set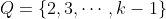 where
where 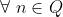 , then n > 1 and n has a prime divisor. Now to show that k exists in Q is quite straightforward with the following partition:
, then n > 1 and n has a prime divisor. Now to show that k exists in Q is quite straightforward with the following partition:
If k has no other factors than k or 1, then k is trivially in Q.
If k is nonprime, then k will have a factor w such that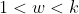 , thus
, thus 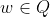 by the inductive hypothesis.
by the inductive hypothesis.
hence
Next method is to show a even stronger result, in other words, the fundmental theorem of arithmetic.
Assume that there are numbers which can not be expressed as a product of primes. Let the smallest possible number of this kind be .
.
 can not be
can not be 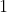 since
since 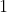 is neither composite nor prime.
is neither composite nor prime.  can not be prime since the PPF of a prime number is just itself. Thus
can not be prime since the PPF of a prime number is just itself. Thus  must be a composite number.
must be a composite number.
Let the composition of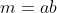 where
where 
Since was the smallest number that can not be expressed as a product of primes, this means
was the smallest number that can not be expressed as a product of primes, this means  and
and  can be expressed as a product of primes and consequently we get
can be expressed as a product of primes and consequently we get 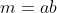 where
where  and
and  can be both expressed as primes. Contradiction!
can be both expressed as primes. Contradiction!
Thus can also be expressed as a product of primes.
can also be expressed as a product of primes.
Lemma 1: If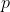 is a prime and
is a prime and 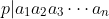 then
then 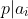 for some
for some 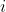 .
.
Lemma 2: If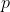 and
and 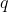 are primes and
are primes and  is a natural number and
is a natural number and 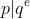 then
then 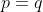 .
.
Let's assume that for some number that there are
that there are 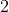 (at least) ways of expressing its PPF.
(at least) ways of expressing its PPF.

Clearly for all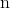 ,
, 

By Lemma 1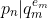 for any
for any  .
.
By Lemma 2
This means that for all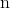 and all
and all  there are values of
there are values of 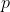 which equals to those of
which equals to those of 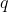 . For example,
. For example, 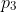 could equal to
could equal to 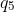 , or
, or 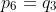 etc. This also means we have created a bijection between
etc. This also means we have created a bijection between 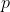 and
and 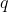 such that
such that 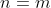 .
.
Therefore if the number has
has 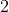 PPF's then the prime number 'base' will be exactly the same, the only different would be in the powers, namely
PPF's then the prime number 'base' will be exactly the same, the only different would be in the powers, namely 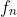 and
and 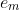 .
.
Now since each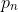 has a corespondent equivalent
has a corespondent equivalent 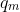 we can rewrite
we can rewrite  as:
as:


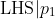 however
however 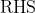 can not be divided by
can not be divided by 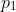 unless for some
unless for some 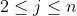 such that
such that 
But since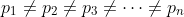 we have a contradiction.
we have a contradiction.
There is a stronger result, that every natural number greater than 1 has a prime divisor. Anyhow, several methods, first as per the question states:New question: Prove by induction that every natural number greater than 2 has a prime divisor.
Assume a set
If k has no other factors than k or 1, then k is trivially in Q.
If k is nonprime, then k will have a factor w such that
hence
Next method is to show a even stronger result, in other words, the fundmental theorem of arithmetic.
Assume that there are numbers which can not be expressed as a product of primes. Let the smallest possible number of this kind be
Let the composition of
Since
Thus
Lemma 1: If
Lemma 2: If
Let's assume that for some number
Clearly for all
By Lemma 1
By Lemma 2
This means that for all
Therefore if the number
Now since each
But since
lolcakes52
Member
- Joined
- Oct 31, 2011
- Messages
- 283
- Gender
- Undisclosed
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Question 1: ß and ∂ are complex roots of the equation x^3 + 5x + 1=0. Show that the other root is -1/|ß|^2
Question 2: Show that ß∂ is a root of the equation x^3 -5x^2 -1=0.
Question 1: ß and ∂ are complex roots of the equation x^3 + 5x + 1=0. Show that the other root is -1/|ß|^2
Question 2: Show that ß∂ is a root of the equation x^3 -5x^2 -1=0.
