Niqqa, that's what i'm suppose to be saying.What why is everyone so smart.
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2012 Year 9 &10 Mathematics Marathon (2 Viewers)
- Thread starter TerenceM
- Start date
Why?I'm losing hope.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Young ones if you spend time investing in your interests, you will always get something in return + interests
If you plant the seed, water it and take care of it, you will get a harvest.
If you plant the seed, water it and take care of it, you will get a harvest.
Yeah well i try to do maths and I get nothing in return except marks reading 7/20!Young ones if you spend time investing in your interests, you will always get something in return + interests
If you plant the seed, water it and take care of it, you will get a harvest.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Because you don't have heart/consistency/invested timeYeah well i try to do maths and I get nothing in return except marks reading 7/20!
Without struggle there is no progress young Fawn
I disagree - I think fawun has all of these things. I think she needs a better teacher and better instruction.Because you don't have heart/consistency/invested time
Without struggle there is no progress young Fawn
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
I disagree - I think fawun has all of these things. I think she needs a better teacher and better instruction.
Fair enough.
Fawun just saying, go on skype. I'll give you the easiest way to get that answer that I found. We're talking about that petal question from Enoilgam right?None of that registered in my brain
but then again it's 1AM and who the hell is thinking about maths at 1AM?
Can you pm me? I'm on my phone and it doesnt have skype lolFawun just saying, go on skype. I'll give you the easiest way to get that answer that I found. We're talking about that petal question from Enoilgam right?
I'll send it later tonight. Got some homework to catch up on, music examinations next Saturday and I'm writing up a maths exam currently.Can you pm me? I'm on my phone and it doesnt have skype lol
HSC2014
Member
- Joined
- Jul 30, 2012
- Messages
- 398
- Gender
- Male
- HSC
- N/A
*Reposting question for others who might want to find petal question
http://community.boredofstudies.org/attachment.php?attachmentid=26350
Fawun, here's a hint. The area of the shaded parts is 100(the square) - (the middle of the petals) - (the corner of the boxes), which should be pretty straight forward. Your goal in this case is to find the middle and the corners' areas.
http://community.boredofstudies.org/attachment.php?attachmentid=26350
Fawun, here's a hint. The area of the shaded parts is 100(the square) - (the middle of the petals) - (the corner of the boxes), which should be pretty straight forward. Your goal in this case is to find the middle and the corners' areas.
hamster-lol
Member
- Joined
- Sep 26, 2012
- Messages
- 41
- Gender
- Male
- HSC
- 2013
You could make the observation that the area of the white outer is equal to the area of the white inner.Cheers have fun (thought last question referred to all of the nonshaded instead of within the box...
bad wording of question tbhView attachment 26519
hamster-lol
Member
- Joined
- Sep 26, 2012
- Messages
- 41
- Gender
- Male
- HSC
- 2013
If you know probability, here is a question I posted in the year 11 marathon.
a) Let = 1 + 2 + 3 + ... + n)
This is) expressed in ascending order. By considering
expressed in ascending order. By considering ) in descending order show that
in descending order show that
 = \frac{1}{2}n(n+1))
b) Consider a bag. This bag has every single letter of the alphabet in it, and only one of each letter so that there are 26 letters in the bag. Let the probability of picking the letter 'z' out of the bag be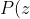)
Now consider another bag, called bag 2. This bag contains 1 A, 2 B's, 3 C's, and so on, up to 26 Z's.
Show that none of the letters in bag 2 have the same probability of being pulled out as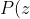)
a) Let
This is
b) Consider a bag. This bag has every single letter of the alphabet in it, and only one of each letter so that there are 26 letters in the bag. Let the probability of picking the letter 'z' out of the bag be
Now consider another bag, called bag 2. This bag contains 1 A, 2 B's, 3 C's, and so on, up to 26 Z's.
Show that none of the letters in bag 2 have the same probability of being pulled out as
ganji
The Juggernaut
- Joined
- Apr 19, 2012
- Messages
- 18
- Gender
- Male
- HSC
- 2014
Here is an interesting question from my maths olympiad. Hint: think about patterns, fairly straightforward once you get it
A positive integer is said to be partitioned if expressed in the form n = x1 +x2 + ... +xk,
where k >= 1 and each of x1, x2, ... , xk is a positive integer. Assuming that order is
signicant (so that, for example, 1 + 2 and 2 + 1 are dierent partitions of 3), determine
in terms of n the number of ways of partitioning n.
A positive integer is said to be partitioned if expressed in the form n = x1 +x2 + ... +xk,
where k >= 1 and each of x1, x2, ... , xk is a positive integer. Assuming that order is
signicant (so that, for example, 1 + 2 and 2 + 1 are dierent partitions of 3), determine
in terms of n the number of ways of partitioning n.
Last edited:
If you know probability, here is a question I posted in the year 11 marathon.
a) Let
This isexpressed in ascending order. By considering
in descending order show that
b) Consider a bag. This bag has every single letter of the alphabet in it, and only one of each letter so that there are 26 letters in the bag. Let the probability of picking the letter 'z' out of the bag be
Now consider another bag, called bag 2. This bag contains 1 A, 2 B's, 3 C's, and so on, up to 26 Z's.
Show that none of the letters in bag 2 have the same probability of being pulled out as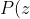)

GG, just replace "a" with "1" and "d" with "n"
LOL, please ban kazemagic - he be cheating. Also, was this question legit in the AMO? I don't recall it being this recent.
GG, just replace "a" with "1" and "d" with "n"


