-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2022 Physics QAT MCQ Doubt (1 Viewer)
chilli 412
oo la la
- Joined
- Apr 13, 2022
- Messages
- 249
- Gender
- Male
- HSC
- 2023
how could velocity be upwards if she is being displaced in the downwards direction over a period of time after opening her parachute?
Run hard@thehsc
Well-Known Member
- Joined
- Oct 7, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2022
I feel like its A as well - C could be true in the instance that the air resistance is greater than the weight force
Bob99
temporarylol hater
- Joined
- Apr 1, 2022
- Messages
- 228
- Gender
- Male
- HSC
- 2022
some other questions also had questionable solutions in this exam so i think the answers are wrong for this question.how could velocity be upwards if she is being displaced in the downwards direction over a period of time after opening her parachute?
Bob99
temporarylol hater
- Joined
- Apr 1, 2022
- Messages
- 228
- Gender
- Male
- HSC
- 2022
I don't think air resistance has the ability to change the direction of the person parachuting, think of it as water, how you slow down when you're walking in it, if the water was very thick (aka more air resistance), it's not going to make you go the other direction. And it's just a resistive force like friction. Too much friction is not going to send your car going the other direction.I feel like its A as well - C could be true in the instance that the air resistance is greater than the weight force
I think the answer should be B (downward acceleration, downward speed) - please see my reasoning below (apologies for the lengthy explanation, but I think this question is a bit subtle / confusing so I spelled out my reasoning in detail).
EDIT: Note that this explanation assumes that "terminal velocity" refers to the terminal velocity of the parachutist plus the parachute combined, rather than the parachutist by themselves. (See Someth1ng's post further below).
Direction of velocity
I agree with Bob here.
V must be pointing down - there is no way the opening the parachute will send the person flying upwards (no need to appeal to physics or mathematics here - just picture it in your head and you can see that it is absurd). Even if air resistance somehow exceeds the weight force, it wouldn't be enough to change the direction of the velocity (the best you could do is get the velocity to slow down to asympotically approach 0 under any physically plausible model for air resistance, since the air reistance also goes to zero when the velocity goes to zero).
Direction of acceleration
For purely illustrative purposes, assume that air resistance is given by then the net force (at the instant the parachute is unfurled) will be
then the net force (at the instant the parachute is unfurled) will be 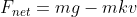 . I am taking the sign convention that down is positive (so g,k,v >0).
. I am taking the sign convention that down is positive (so g,k,v >0).
In this case the direction of the acceleration will depend on whether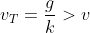 or
or  at the time of unfurling the parachute, where
at the time of unfurling the parachute, where 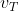 denotes the terminal velocity.
denotes the terminal velocity.
In other words, there are 2 cases (in any reasonable model that we choose for air resistance):
1. If the parachutist unfurls before they attain their terminal velocity, then they will continue speeding up downards (i.e. downward acceleration, since downward velocity is increasing) until they reach that terminal velocity.
2. If they unfurl after reaching terminal velocity and are travelling faster than the terminal velocity at the moment of unfurling, then they will slow down (i.e. upward acceleration, since downward velocity is decreasing) until they reach that terminal velocity.
In the question, we are told that Option 1 is true (wording is not clear but in my opinion it is implied by the phrase "opening her parachute...before she reaches terminal speed" ). Therefore acceleration is also downward.
EDIT: Note that this explanation assumes that "terminal velocity" refers to the terminal velocity of the parachutist plus the parachute combined, rather than the parachutist by themselves. (See Someth1ng's post further below).
Direction of velocity
I agree with Bob here.
V must be pointing down - there is no way the opening the parachute will send the person flying upwards (no need to appeal to physics or mathematics here - just picture it in your head and you can see that it is absurd). Even if air resistance somehow exceeds the weight force, it wouldn't be enough to change the direction of the velocity (the best you could do is get the velocity to slow down to asympotically approach 0 under any physically plausible model for air resistance, since the air reistance also goes to zero when the velocity goes to zero).
Direction of acceleration
For purely illustrative purposes, assume that air resistance is given by
In this case the direction of the acceleration will depend on whether
In other words, there are 2 cases (in any reasonable model that we choose for air resistance):
1. If the parachutist unfurls before they attain their terminal velocity, then they will continue speeding up downards (i.e. downward acceleration, since downward velocity is increasing) until they reach that terminal velocity.
2. If they unfurl after reaching terminal velocity and are travelling faster than the terminal velocity at the moment of unfurling, then they will slow down (i.e. upward acceleration, since downward velocity is decreasing) until they reach that terminal velocity.
In the question, we are told that Option 1 is true (wording is not clear but in my opinion it is implied by the phrase "opening her parachute...before she reaches terminal speed" ). Therefore acceleration is also downward.
Last edited:
Bob99
temporarylol hater
- Joined
- Apr 1, 2022
- Messages
- 228
- Gender
- Male
- HSC
- 2022
Thank you for the great explanation!!!I think the answer should be B (downward acceleration, downward speed) - please see my reasoning below (apologies for the lengthy explanation, but I think this question is a bit subtle / confusing so I spelled out my reasoning in detail).
Direction of velocity
I agree with Bob here.
V must be pointing down - there is no way the opening the parachute will send the person flying upwards (no need to appeal to physics or mathematics here - just picture it in your head and you can see that it is absurd). Even if air resistance somehow exceeds the weight force, it wouldn't be enough to change the direction of the velocity (the best you could do is get the velocity to slow down to asympotically approach 0 under any physically plausible model for air resistance, since the air reistance also goes to zero when the velocity goes to zero).
Direction of acceleration
For purely illustrative purposes, assume that air resistance is given bythen the net force (at the instant the parachute is unfurled) will be
. I am taking the sign convention that down is positive (so g,k,v >0).
In this case the direction of the acceleration will depend on whetheror
at the time of unfurling the parachute, where
denotes the terminal velocity.
In other words, there are 2 cases (in any reasonable model that we choose for air resistance):
1. If the parachutist unfurls before they attain their terminal velocity, then they will continue speeding up downards (i.e. downward acceleration, since downward velocity is increasing) until they reach that terminal velocity.
2. If they unfurl after reaching terminal velocity and are travelling faster than the terminal velocity at the moment of unfurling, then they will slow down (i.e. upward acceleration, since downward velocity is decreasing) until they reach that terminal velocity.
In the question, we are told that Option 1 is true (wording is not clear but in my opinion it is implied by the phrase "opening her parachute...before she reaches terminal speed" ). Therefore acceleration is also downward.
The confusing aspect of this question would definitely be the terminal velocity which makes everything harder.
chilli 412
oo la la
- Joined
- Apr 13, 2022
- Messages
- 249
- Gender
- Male
- HSC
- 2023
still a bit confused with acceleration being downwards because if we take her velocity before deploying the parachute to beI think the answer should be B (downward acceleration, downward speed) - please see my reasoning below (apologies for the lengthy explanation, but I think this question is a bit subtle / confusing so I spelled out my reasoning in detail).
Direction of velocity
I agree with Bob here.
V must be pointing down - there is no way the opening the parachute will send the person flying upwards (no need to appeal to physics or mathematics here - just picture it in your head and you can see that it is absurd). Even if air resistance somehow exceeds the weight force, it wouldn't be enough to change the direction of the velocity (the best you could do is get the velocity to slow down to asympotically approach 0 under any physically plausible model for air resistance, since the air reistance also goes to zero when the velocity goes to zero).
Direction of acceleration
For purely illustrative purposes, assume that air resistance is given bythen the net force (at the instant the parachute is unfurled) will be
. I am taking the sign convention that down is positive (so g,k,v >0).
In this case the direction of the acceleration will depend on whetheror
at the time of unfurling the parachute, where
denotes the terminal velocity.
In other words, there are 2 cases (in any reasonable model that we choose for air resistance):
1. If the parachutist unfurls before they attain their terminal velocity, then they will continue speeding up downards (i.e. downward acceleration, since downward velocity is increasing) until they reach that terminal velocity.
2. If they unfurl after reaching terminal velocity and are travelling faster than the terminal velocity at the moment of unfurling, then they will slow down (i.e. upward acceleration, since downward velocity is decreasing) until they reach that terminal velocity.
In the question, we are told that Option 1 is true (wording is not clear but in my opinion it is implied by the phrase "opening her parachute...before she reaches terminal speed" ). Therefore acceleration is also downward.
so
someth1ng
Retired Nov '14
This is a bad question for several reasons. It needs to specify which terminal speed (i.e. with or without the parachute deployed).View attachment 36346
Answers say C
I think it has to be A.
Someone pls come to the rescue with the correct explanation.
We can start with velocity, V, which will always be down because the skydiver will always be in free fall (ignoring horizontal movement).
If the parachute is deployed just before the skydiver reaches non-parachute terminal velocity but faster than parachute terminal velocity, then acceleration will be up. Essentially, the downward velocity is decreasing, which is her gaining velocity in the upward direction.
If the parachute is deployed before the skydiver reaches parachute terminal velocity, such as almost immediately after leaving the plane, then net acceleration will still be down because she hasn't reached parachute terminal velocity. If she were traveling faster than the parachute terminal velocity, then she will slow down.
Therefore, IMO, you can argue for A and B.
Last edited:
I don't think this is true in general. Suppose that they opened the parachute immediately when they jump (i.e. at zero downward velocity). Therefore in spite of the parachute being opened, their downward speed will still continue to increase because their weight force exceeds air resistance.still a bit confused with acceleration being downwards because if we take her velocity before deploying the parachute to be, and velocity after deploying the parachute as
,and going off the fact that deploying a parachute would decrease her velocity (even if she is yet to reach terminal velocity)
so, wouldnt that mean acceleration is opposing her downwards movement as
(and we are defining downwards to be positive) ?
chilli 412
oo la la
- Joined
- Apr 13, 2022
- Messages
- 249
- Gender
- Male
- HSC
- 2023
that makes sense but because the question says "the sky diver is falling downward when she opens her parachute" shouldnt we assume that she has not just deployed her parachute directly after jumping?I don't think this is true in general. Suppose that they opened the parachute immediately when they jump (i.e. at zero downward velocity). Therefore in spite of the parachute being opened, their downward speed will still continue to increase because their weight force exceeds air resistance.
Sure fair enough but that was just an extreme example - I don't actually need a zero velocity for the argument to work. For instance, I could assume that she opens the parachute when she is falling downard at 0.01 m/s (i.e. something definitely below the terminal velocity). In that case, the parachutist would still accelerate downwards after opening.that makes sense but because the question says "the sky diver is falling downward when she opens her parachute" shouldnt we assume that she has not just deployed her parachute directly after jumping?
wizzkids
Well-Known Member
- Joined
- Jul 13, 2016
- Messages
- 417
- Gender
- Undisclosed
- HSC
- 1998
Exam technique. Draw a graph of what you expect the velocity of the skydiver to look like. Transfer any data that is provided onto the graph. Then think about acceleration as the derivative of velocity with respect to time, ie. acceleration is the slope of the velocity versus time graph.
Then you should have no trouble getting the correct answer.

Then you should have no trouble getting the correct answer.

